Collision Energy

 The kinetic energy between two colliding particles can be expressed in terms of center of mass and relative velocity by

\[ E_k = \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2v_2^2 = \frac{1}{2} M v_c^2 + \frac{1}{2} \mu v_r^2 , \]

a sum of a center-of-mass term and a relative momentum term.

where $M$, $v_c$, $\nu$, and $v_r$ are given by

\[ M = (m_1+m_2) ; \]

\[ \mathbf{v_c} = \frac{m_1 \mathbf{v_1} + m_2 \mathbf{v_2}}{m_1 +m_2} ;\]

\[ \mu = \frac{m_1 m_2}{m_1 + m_2} ;\]

\[ \mathbf{v_r} = \mathbf{v_1} - \mathbf{v_2} .\]

$\frac{1}{2} \mu v_r^2$ is called collision energy.

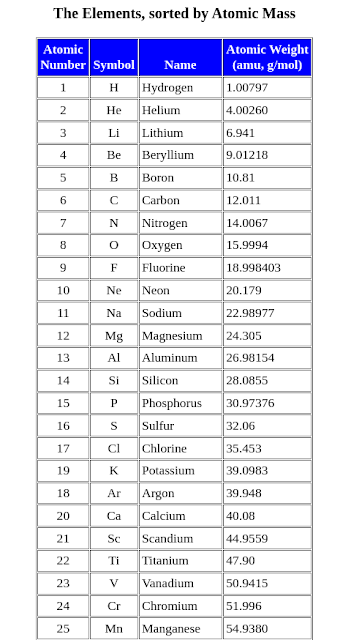
amu is short for atomic mass unit. Protons have a positive electrical charge of one (+1) and a mass of 1 atomic mass unit (amu), which is about 1.67×10−27 kilograms.

Reference:

https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Map%3A_Physical_Chemistry_for_the_Biosciences_(Chang)/02%3A_Properties_of_Gases/2.8%3A_Molecular_Collisions_and_the_Mean_Free_Path

https://web.chem.ox.ac.uk/teaching/Physics%20for%20CHemists/Mechanics/Collisions.html

https://www.angelo.edu/faculty/kboudrea/periodic/structure_mass.htm